Kalkulus - Diagram Venn

1. Definisi Diagram Venn :

            Alat untuk menggambarkan hubungan antara himpunan-himpunan

            Himpunan yang dimaksud digambarkan dengan lingkaran sedangkan himpunan Semesta digambarkan dengan 4 persegi panjang

2. Operasi antar Himpunan :

1.      Gabungan ( Union ) ® symbol  È

Contoh : S = { a, b, c, d } ;  T = { a, d, e, f }, maka :

               S È T = { a, b, c, d, e, f  }

               S È T = { x | x Î S  atau  x Î T }

2.      Irisan ( intersection ) ® symbol  Ç

Contoh : P = { a, b, c, d } ; R = { a, d, e, f } ;  Q = { h, i, j, k  }, maka :

               P Ç R = { a, d }

               P Ç R = { x | x Î P dan x Î R }     

               P Ç Q =  f …… saling asing/disjoint/kosong

               R Ç Q =  f …… saling asing/disjoint/kosong

3.      Komplemen dari S ® symbol S^c

Contoh : S  = { 1, 2, 3 }, maka :

               S^c = {4, 5, 6……}

               S^c = { 0,-1,-2…..}

4.      Selisih ® X – Y

Contoh :  X = { 10, 20, 30, 40, 50 } ; Y = {10, 30, 60 }, maka :

                X – Y = { 20, 40, 50 }

5.      Selisih Simetri ® symbol Ñ

Contoh : A = { 2, 3, 4, 6 } ; B = { 1, 3, 4, 5, 6 }, maka :

               A Ñ B = ( A È B ) – ( A Ç B )

                          = {1, 2, 3, 4, 5, 6 } – { 3, 4, 6 }

                          =    { 1, 2, 5 }

Atau        A Ñ B = ( A – B ) È ( B – A )

                          = { 2 } È { 1, 5 }

                          =  { 1, 2, 5 }

6.      Hasil kali cartesius dari 2 himpunan A dan B ® symbol  x

A x B = { ( x,y ) | x Î A,  y Î B  } ® x dan y pasangan berurut

Contoh : A = { a, b, c }

               B = { 1, 2 }

               A x B = { (a,1), (a,2), (b,1), (b,2), (c,1), (c,2) }

               B x A = { (1,a), (1,b), (1,c), (2,a), (2,b), (2,c) }

               A x B ¹ B x A

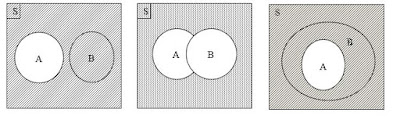
3.     Diagram Venn untuk Operasi-operasi pada Himpunan :

1. Diagram Venn untuk operasi Gabungan

2. Diagram Venn untuk operasi Irisan 

3. Diagram Venn untuk operasi Selisih (A-B)

4. Diagram Venn untuk komplemen himpunan (A^C)

     5. Diagram Venn untuk operasi Selisih Simetri (AÑB)

Materi ini dapat anda download disini, didalamnya juga terdapat beberapa soal-soal latihan yang dapat anda pelajari dan kerjakan.